Pour prendre une bonne décision, cela peut nécessiter de résoudre un problème d'optimisation combinatoire, c'est-à-dire trouver la meilleure combinaison possible parmi un très grand nombre de possibilités. Ces problèmes d'optimisation combinatoire apparaissent dans de nombreux domaines comme la logistique, les télécommunications, la chimie ou bien la bio-informatique.

Un exemple de problème d'optimisation combinatoire que l'on peut rencontrer dans la vie réelle  peut être la création d'un emploi du temps pour une université. Pour qu'un emploi du temps soit réussi, il faut qu'il satisfasse au mieux les préférences des enseignants et des étudiants. Notamment, cet emploi du temps doit idéalement laisser le moins de plages horaires sans cours  au milieu de la journée tout en satisfaisant un certain nombre de contraintes comme garantir, par exemple, que deux cours différents n’aient pas lieu en même temps avec le même enseignant ni dans la même salle de cours. On sait à quel point créer un tel emploi du temps qui respecte toutes les contraintes peut être un véritable casse-tête. C'est pourquoi il existe des programmes informatiques qui mettent en œuvre des algorithmes de résolution permettant de trouver automatiquement l’emploi du temps le plus optimal possible.

Lorsque le problème peut être exprimé avec des formules mathématiques, on parle alors d’optimisation « boîte blanche ». C'est le cas du problème de création d'emplois du temps évoqué ci-dessus pour lequel toutes les variables du problèmes sont connues et pour lequel l’impact de déplacer tel ou tel créneau de cours sur la qualité globale de l’emploi du temps est directement mesurable.

Dans le cas où il n'y a pas d'expressions mathématiques explicites permettant de connaître directement le résultat de la combinaison des variables du système que l’on évalue, il s’agit d'optimisation dite « boîte noire ». C'est ce qui peut arriver par exemple quand l’objectif de l’optimisation est le résultat de la simulation d’un système complexe. Il faut attendre que chaque simulation soit terminée pour obtenir le résultat d’une configuration testée. Un exemple de problème d'optimisation « boîte noire » peut être l'optimisation des positions des arrêts de bus dans une ville pour maximiser la qualité du service. Évaluer une configuration donnée des positions des arrêts de bus nécessite de lancer un modèle de simulation du trafic urbain de la ville, ce qui peut être coûteux en terme de temps de calcul. On voudrait dans ce cas trouver la meilleure configuration possible des arrêts de bus en lançant le moins possible de simulations, c’est-à-dire en évaluant le moins de configurations possibles.

Ainsi, pour analyser les particularités d’un problème d’optimisation et sa difficulté, on peut le représenter sous la forme d’un paysage adaptatif. Ce paysage adaptatif, visualisé sous la forme d'une carte topographique, est une représentation de la qualité de chacune des combinaisons possibles du problème. Cette représentation vient du domaine de la biologie pour exprimer la relation entre les génotypes des individus, c’est à dire leur combinaison de gènes, et leur qualité d’adaptation dans un environnement donné.

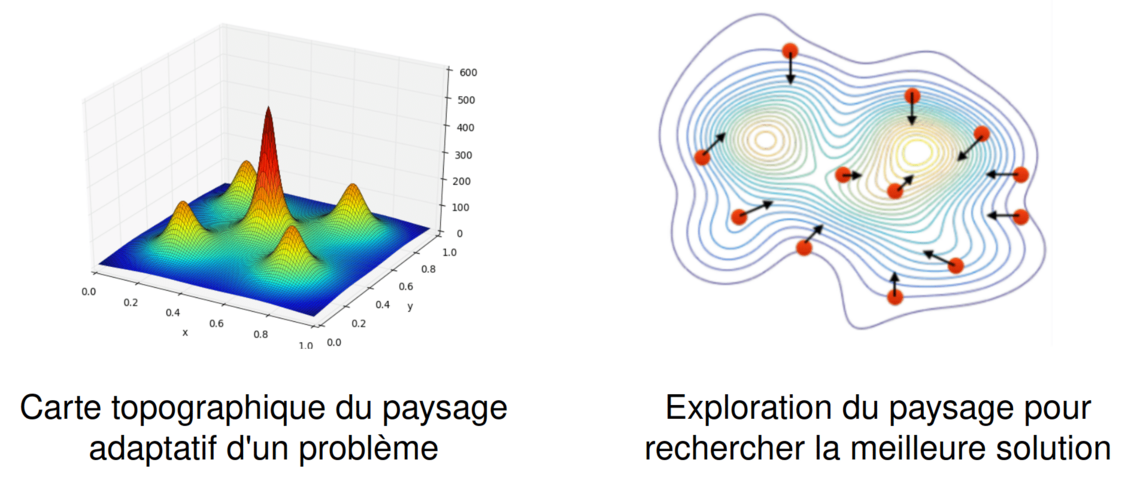
Pour résoudre le problème d’optimisation, il s’agit d’explorer le paysage adaptatif ainsi défini jusqu’à trouver la solution de la meilleure qualité possible, c'est-à-dire la plus haute valeur en rouge comme présenté sur le croquis de gauche de l’image ci-dessus. On voit sur le croquis de droite comment un algorithme peut faire évoluer des solutions candidates, ou "individus", dans le paysage adaptatif, à la recherche de meilleures solutions.

Étant donné les enjeux liés à la résolution efficace de problèmes d’optimisation combinatoire, leur difficulté, et surtout les contraintes de temps de résolution, une grande variété d’algorithmes ont été conçus dans la communauté scientifique pour les résoudre le plus efficacement possible. Or, si l’on considère une famille de problèmes suffisamment large, il a été constaté qu'aucun algorithme ne domine clairement tous ses concurrents sur tous les problèmes. Au contraire, la diversité des paysages adaptatifs de problèmes d'optimisation nécessite une variété d'algorithmes pour les résoudre efficacement. Cependant, le développement d'un algorithme efficace pour résoudre chaque type de problème est une tâche difficile qui requiert un haut niveau d'expertise.

Dans le projet DeepMeta, que nous avons mené au laboratoire informatique LERIA de l’université d’Angers, de 2023 à 2024, et soutenu par le dispositif régional « Étoiles Montantes en Pays de la Loire », nous avons développé une nouvelle approche fondée sur des modèles d’intelligence artificielle qui permet de faire émerger de nouveaux algorithmes de résolution de problèmes combinatoires. Les résultats obtenus montrent qu’il est possible de découvrir automatiquement de nouvelles stratégies de résolution différentes et adaptées à chaque classe de problème rencontrée, meilleures que celles qui auraient pu être conçues « à la main » par des experts du domaine.