Contexte : De nos jours, le progrès constant des appareils de mesure (sondes, capteurs, questionnaires en ligne, etc. ), combiné aux importantes capacités informatiques, favorise l’apparition de tableaux de données de plus en plus grands et complexes. L’analyse de ces immenses tableaux de données pose de nouveaux défis aux chercheurs de tous les domaines (biologistes, épidémiologistes, chimistes, etc.). Depuis quelques années, le terme de données massives (en anglais big data) est devenu populaire pour désigner ces nouvelles données. Des analyses statistiques avancées ont été développées, permettant de représenter ces gigantesques tableaux de manière simplifiée tout en gardant le maximum d'informations. Ces procédures sont appelées analyses exploratoires (par ex. l’ACP [Pearson, 1901; Hotelling, 1933]), car elles sont utilisées lorsqu’on dispose de peu, voire d’aucune information sur le jeu de données initial. Elles servent donc à explorer les données pour en révéler leurs secrets.

Problématique : Cependant, la présence de données de natures très différentes pose un problème. En effet, certaines informations sont mesurées par des chiffres (appelées données numériques) et d’autres par des lettres (appelées données catégorielles). La plupart des indices statistiques sont calculables sur les chiffres : moyenne, écart-type, ou des analyses plus poussées comme les analyses exploratoires. En revanche, il est impossible de faire de tels calculs sur des lettres … Comment analyser ensemble des données si différentes ? 

Un exemple concret : Prenons des exemples concrets pour éclairer le sujet. Dans le cadre d’études médicales, il est courant de suivre un ensemble de patients en mesurant des données telles que l’âge ou le poids (données numériques, des chiffres). De plus, les chercheurs suivent également le tabagisme des patients : non-fumeur, fumeur, ancien fumeur, fumeur passif [Lavoie-Charland et al., 2013], c’est-à-dire des lettres. À cette complexité s'ajoutent des données à mi-chemin entre les chiffres et les lettres : des données catégorielles ordonnées (dites ordinales). Par exemple, la mesure de la sévérité d’une maladie : pas de symptômes < symptômes légers < symptômes modérés < symptômes sévères). La Figure 1 illustre les différents exemples présentés. 

Figure 1 : Représentation schématique des différentes données et leurs natures.

Solution proposée : Après des recherches scientifiques, la solution envisagée fut d’attribuer des valeurs numériques (des chiffres) aux données catégorielles (les lettres). Ce procédé ancien porte le nom de “quantification” [Bock, 196; De Leeuw, 1980]. Il permet d’attribuer à toutes les données (même catégorielles) des valeurs numériques de la meilleure façon possible. On obtient ainsi un nouveau jeu de données entièrement composé de chiffres, qu’il est désormais aisé d’analyser en utilisant les procédures standards. Ainsi, au cours de ma thèse, réalisée à Oniris (Nantes) au sein de l’unité StatSC et en partenariat avec l'ANSES, j'ai couplé un algorithme de quantification avec une méthode d’analyse très populaire et considérée comme standard de nos jours : l’ACP [Pearson, 1901; Hotelling, 1933], formant ainsi une ACP avec quantification [De Leeuw, 2013].

Application à des problématiques actuelles : L’application de cet algorithme a déjà permis d’analyser des jeux de données complexes dans divers domaines d’études. Par exemple, dans le domaine de l'épidémiologie, il a été utilisé pour analyser un jeu de données massif concernant l’étude de la maladie du COVID-19 [Paries, 2023] (cohorte de données intitulée CURIE-O-SA [Anna et al., 2021]). Les données composées de 4 383 individus et 19 variables de natures différentes ont été explorées en utilisant la méthode d'ACP avec quantification. Certaines d'entre elles sont numériques (des chiffres), par exemple la quantité d’anticorps présents dans le sang, d'autres sont catégorielles (des lettres), par exemple la vaccination contre la maladie : non vacciné < vacciné une fois < vacciné deux fois. Il a ainsi été mis en évidence que le groupe des individus à la fois vaccinés et infectés par le virus SARS-CoV-2 (en rouge sur la Figure 2) était mieux protégé, en termes d’anticorps, contre la maladie que les individus uniquement infectés (en orange) ou uniquement vaccinés (en vert). 

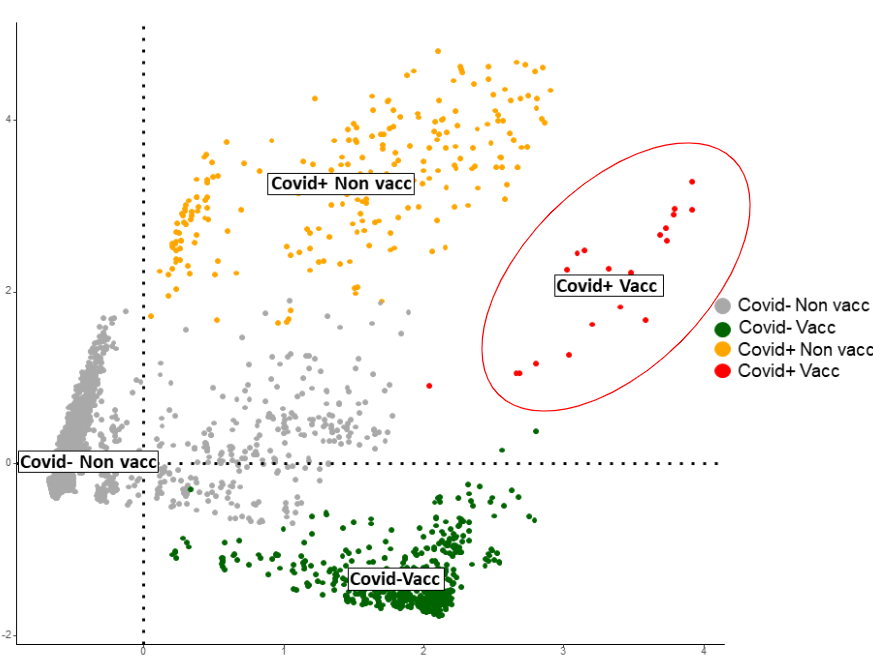
Figure 2 : Données cohorte CURIE-O-SA ; 4383 individus ; Exemple de résultat : visualisation des des individus. Méthode MBPCAOS. On remarque en rouge un groupe d’individus distinct des autres et mieux protégé.

Conclusion : Les statistiques, en tant que discipline générale applicable à tous les domaines, jouent un rôle essentiel dans l'avancement de nombreuses autres disciplines scientifiques. Ainsi, pour en faire profiter le plus grand nombre, l’algorithme développé durant ma thèse a été implémenté avec un langage open source (R) et est accessible à tous sur un répertoire GitHub : https://github.com/martinparies/PCA.OS.

Ecrit par Martin PARIES, docteur en statistiques appliquées (2024).

Références :

Anna, F., S. Goyard, A. I. Lalanne, F. Nevo, M. Gransagne, P. Souque, D. Louis, V. Gillon, I. Turbiez, F. Bidard, A. Gobillion, A. Savignoni, M. Guillot-Delost, F. Dejardin, E. Dufour, S. Petres, O. Richard-Le Goff, Z. Choucha, O. Helynck, Y. L. Janin, N. Escriou, P. Charneau, F. Perez, T. Rose, and O. Lantz (2021, January). High seroprevalence but short-lived immune response to SARS-CoV-2 infection in Paris. European Journal of Immunology 51 (1), 180–190.

Bock, R. D. (1960). Methods and applications of optimal scaling. The University of North Carolina Psychometric Laboratory Research Memorandum 25.

De Leeuw, J. and J. Van Rijckevorsel (1980). HOMALS and PRINCALS-Some generalizations of principal components analysis. 2, 231–242. Publisher : Amsterdam : North-Holland.

De Leeuw, J. (2013). History of nonlinear principal component analysis. 

Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of educational psychology 24 (6), 417. ISBN : 1939-2176 Publisher : Warwick & York. 

Lavoie-Charland, É., J.-C. Bérubé, M. Laviolette, L.-P. Boulet, and Y. Bossé (2013). Multivariate asthma phenotypes in adults : the quebec city case-control asthma cohort. Open Journal of Respiratory Diseases 2013. 

Paries, M., Vigneau, E., Huneau, A., Lantz, O., & Bougeard, S. (2023). MBPCA-OS: an exploratory multiblock method for variables of different measurement levels. Application to study the immune response to SARS-CoV-2 infection and vaccination. The International Journal of Biostatistics, (0).

Pearson, K. (1901, November). LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 2 (11), 559–572.